Subspace

A Vector Space’s version of a Subset, with some constraints.

While, a subspace does inherit the axioms of a Vector Space. Verifying a subset is a subspace is simpler; A Subset of is a subspace if it is closed within scalar multiplication and vector addition:

Properties

• , i.e. the Span of any subset is identical to itself

Four Fundamental Subspaces

For Matrix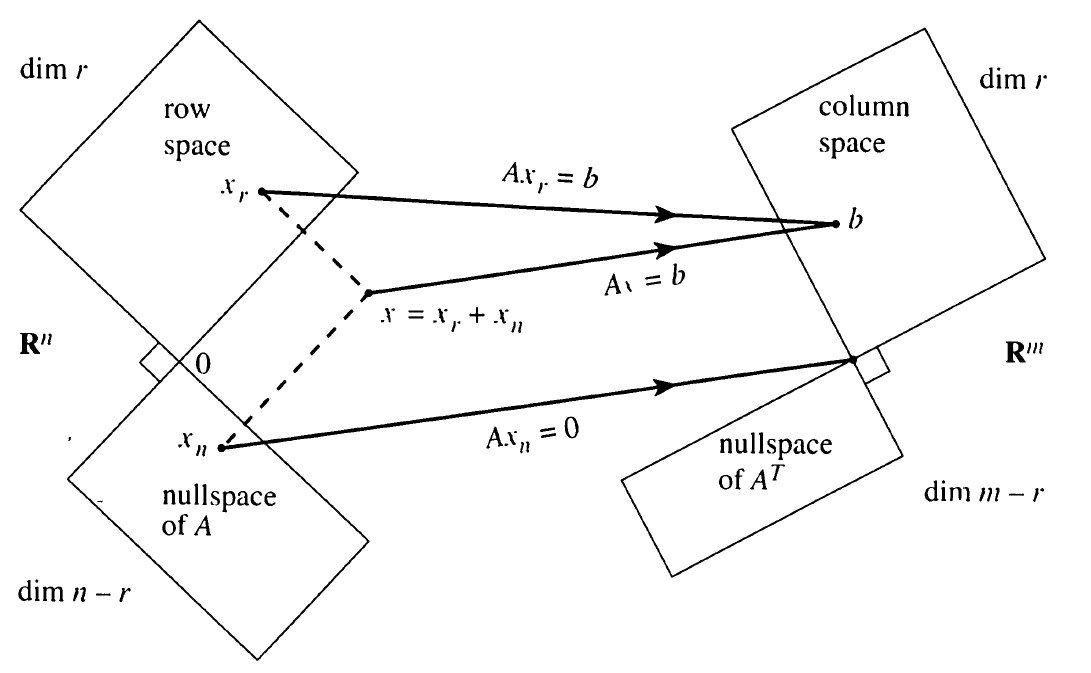

• The Subspaces are linked by the Fundamental Theorem of Linear Algebra
  • Rowspace
  • Nullspace of
  • Columnspace
  • Nullspace of , “Left Nullspace”
• Shows the relationship between the dimensions of the subspaces
• Shows the Morphisms between different subspaces of a matrix
  • Show existence of solutions:
• Shows the Orthogonality relationship between related subspaces of a matrix