Propositional Logic

Proposition

A proposition is a Declarative Sentence that is either true or false, but not both.

Link to original

Declarative Sentence

A declarative sentence is a sentence that declares something falsifiable.

Link to original

Examples:

7 - 4 = 3 prop

Odin is on our side prop

What is a Viking’s favorite food? not prop

Every Saxon is under attack. prop

x+y=3 not prop, because x and y vary

Propositional Variables are variables used to denote propositions.

• Typically: p, q, r, s, …
• never use capitals as they are reserved for propositional functions

Negation

Negation of denoted by

• *You must use to mean “not”
• same as !

Examples:

1. Ronnie likes Taco Bell : “Ronnie likes Taco Bell” : “It is not the case that Ronnie likes Taco Bell”, “Ronnie does not like Taco Bell”

2. Thor’s hammer is not named Mjölnir always define prop vars as positive as below m: “Thor’s hammer is named Mjolnir” Negate original: “Double negation rule”

Truth Values and Truth Tables

1. Suppose we have a proposition . Create a truth table for and

T	F
F	T

A conjunction of and is the statement “p and q”

• it is denoted as
• same as &&
• Both p and q must be true for to be true

A disjunction of p and q is the statement “p or q”

• it is denoted as
• it is same as ||
• is true whenever p is true, q is true, or both p, q are true

Examples:

: “Ronnie has 3 cats” : “Ronnie does CrossFit”

1. Find Ronnie has 3 cats or Ronnie does CrossFit
2. Find Ronnie does not have 3 cats and Ronnie does CrossFit

The exclusive or of p and q is the statement p XOR q

• Same as ^
• In order to eval to true, p can be true or q can be true, but not both

Conditionals & More!

Let p and q be propositions

• A statement in the form “if p, then q” is called a conditional statement
• written as
• False when p is true and q is false, otherwise true
• p is called the hypothesis, sufficient condition
• q is called the conclusion or the necessary condition
• if sufficient condition happens, then the necessary condition must happen

Truth Tables:

• List all possible combinations of truth values
• If is the # of unique prop vars, then there are rows in the truth table

p	q
T	T	T	T	F	T
T	F	F	T	T	F
F	T	F	T	T	T
F	F	F	F	F	T

• if p, then q
• if p, q
• p is sufficient for q
• q if p
• q when p
• a necessary condition for p is q
• q unless ￢p
• p implies q
• p only if q (follows)
• a sufficient condition for q is p
• q whenever p
• q is necessary for p
• q follows from p
• q provided that p

Converses, Inverses, Contrapositives

Given

1. Converse:
2. Inverse:
3. Contrapositive:

Biconditional

• p iff q
• p q (p q) (q p)

Precedence of Logical Operators

Logic Puzzles

In the Vikings age, there lived 2 types of people

• Vikings, who are honorable and always tell the truth
• Saxons, who are not honorable so they never tell the truth Determine who is a Viking or Saxon between Ragnar and Egbert who say the following: Ragnar: I am a Viking only when Egbert is not ^[only if] Egbert: I am not a Saxon and Ragnar is a Saxon p: Ragnar is a viking, : Ragnar is a saxon q: Egbert is a viking, : Egbert is a saxon Ragnar says: Egbert sats:

p	q				Whether Ragnar statement and identity align	Whether Egbert statement and identity align	Ragnar aligned && Egbert Aligned, i.e. do they go together
T	T	F	F	F	F	F	F
T	F	F	T	T	T	T	T
F	T	T	F	T	F	T	F
F	F	T	T	T	F	T	F
Based on the truth table,

Now same situation, but different statements Ragnar says: We are both Saxons Egbert says: We are both Vikings p: Ragnar is a viking, : Ragnar is a saxon q: Egbert is a viking, : Egbert is a saxon Ragnar says: Egbert says:

p	q
T	T	F	F	F	F	T	T	F
T	F	F	T	F	F	F	T	F
F	T	T	F	F	T	F	F	F
F	F	T	T	T	F	F	T	F
No solution

If solution, “unable to determine”

Loki has heard of your exploits and wishes to honor you with a prize. However, being the deceiver that he is, he requires that you earn your prize by correctly determining which of three Chests actually holds the treasure. Only one Chest holds any treasure but the others are empty. You begin looking at the Chests and notice that Chests 1 and 2 are each inscribed with the message, “This Chest is empty.” The third Chest is inscribed with the message, “The treasure is in Chest 2.” Forseti, an honorable fellow, tells you that only one of these inscriptions are true. Which Chest do you select?

p: Treasure is in chest one q: Treasure is in chest two r: Treasure is in chest two 1: I’m empty () 2: I’m empty () 3: Treasure in 2 ()

1 is true: 2 is true: 3 is true:

Treasure in one

Definitions

Compound proposition: any expression formed from propositional variables using logical operators Tautology: always true compound prop. Contradiction: a compound prop. that is always false Contingency: everything else

Laws

Conditional Disjunction Equivalence

Absorption

Prove Equivalence

A Proof for DeMorgan’s First Law

Law:

p	q
T	T	F	F	T	F	F
T	F	F	T	F	T	T
F	T	T	F	F	T	T
F	F	T	T	F	T	T

Prove logical equivalences without truth tables by using logical equivalences

Show that is a tautology

	Given
	Cond. Disj. Equiv.
	DeMorgan’s
	Asoc. & Comm.
	Negation law
	Domination Law

Satisfiability

A compound proposition is satisfiable if there is an assignment of truth vaues to its variables that make it true (when it is a tautology or contingency) A compound proposition will be unsatisfiable if and only if it is a contradiction

Predicates and Quantifiers

Propositional Logic vs Predicate Logic

Example:

• x > 3
• x is the subject
• “less than 3” is the predicate
  • a property of x
• “x < 3” can be represented by
  • P denotes the predicate, x is the variable
• Let denote

Universal Quantifier

• The universal quantification of P(x) is the statement “P(x) for all values of x in the domain”
• “for all x in P(x)”
• is the universal quantifier

Must include domain in statements

Existential Quantifier

• The existential quantification of P(x) is the proposition: “There exists an element x in the domain such that P(x).”
• “For some”, at least one / it exists

Uniqueness Quantifier

• “There exists a unique”, i.e. only one
• e.g. , due to -3, 3

takes precedent over all logical operators

Quantifiers over Finite Domains

If the domain of a quantifier is finite, then you can convert quantified statements to propositional logic e.g. if domain = {}

Domain Shorthand example

“for all x less than 0, “

De Morgan’s Laws for Quantifiers

Negation	Equivalent Statement	Negation is true when…	Negation is false when…
		P(x) is false for every x	There is an x that makes P(x) true
		There is an x that makes P(x) false	P(x) is true for every x.

Double quant: DeMorgan allows to move neg inside if swap quant. Only have to be same x and y if in same scope. (Like programming)  

Statement	The statement is true when…	The statement is false when…
∀x∀yP(x,y)	P(x,y) is true for all pairs x,y	There is a pair x,y that makes P(x,y) false
∀x∃yP(x,y)	For each x, you can find a y that makes P(x,y) true	There is a value for x such that no value for y can make P(x,y) true
∃x∀yP(x,y)	There is an x that makes P(x,y) true for every y	There is not a single x that makes P(x,y) true for every y
∃x∃yP(x,y)	There is a pair x,y that makes P(x,y) true	There are no pairs x,y that make P(x,y) true

End

Argument

Argument: a set of initial statements, called premises, followed by a conclusion. An argument is valid if and only if in every case where all the premises are true, the conclusion is true. Otherwise, the argument is invalid.

• An argument can be valid even if the conclusion is false. This can occur if one of the premises is false. The requirement here for “valid” is that the conclusion is true when all premises are true.
• To prove a valid argument, show that the conjunction of the premises, leading to the conclusion is a tautology

Argument Name	Logical Representation
Modus Ponens
Modus tollens
Addition
Simplification
Conjunction
Hypothetical syllogism
Disjunctive syllogism
Resolution

Example

Want conclusion to be

Statements	Reasons
	Given
	Given
	Given
	Given
	Simplification on
	Disjunctive Syllogism on and
	Modus Tollens and
	Disjunctive Syllogism on and

Fallacy

Intro to Proofs: Direct Proof

Theorem a statement that can be shown to be true. Proof a valid argument that establishes the truth of a theorem Lemma less important theorems usually used to prove complicated theorems Corollary a theorem that is established directly from a theorem that has been proved Conjecture a statment that is being proposed as true

• Proving one makes it a theorem

Useful definitions and axioms

1. The integer n is even if there exists an integer k such that n = 2k, and 
2. n is odd if there exists an integer k such that n = 2k + 1. 
3. Closure of multiplication in integers:  The product of two integers is an integer.  
4. Closure of addition in integers: The sum of two integers is an integer
5. Closure of subtraction in integers:  The difference of any two integers is an integer
6. There is no closure of division (because of zero)

7. 3-5 above also work for real numbers.  replace all instances of the word integer with real number

8. The real number r is rational if there exist integers p and q with q ≠ 0 such that r = p∕q.
9. A real number that is not rational is called irrational.
10. A number m is a perfect square iff there exists some integer k such that

Proof Format Introduction: Specify the type of proof technique you are using. E.g. I proceed with a direct proof. If proving a theorem in the form of conditional. State “Assume the hyp. Is true” where hyp. Is the hypothesis of the conditional. Outline any other things you may need to use to build this proof. Body: Write your argument for your proof. This step may typically contain multiple parts depending on both the proof technique and the theorem you are proving. Always define the domains of new variables you introduce See each proof technique for specifics. All simplification can be done in a single step. Any argument given should have a reason to go along with it. e.g. Let n be odd. By definition of odd, there’s an integer k such that n = 2k+1. Conclusion. State “Therefore by (insert proof technique)…is proven.” where … was the thing you were proving. Be careful to specify the entire theorem and not just the conclusion.

Direct Proof is a type of proof that directly leads to a conclusion, i.e. . The assumption is that p is true, and we prove that q must follow.

Two Column Proof a proof with statements and reasons.

set of int set of real set of rational set of complex

Example: Give a direct proof of “If n is an even integer then is an even integer”

Pf: I proceed directly and assume is even.

Statement	Reasons
n is even	Premise
Let n = 2k, where	Definition of even
	Square both sides of the equation
	Factoring out a 2
Let for some	Closure of multiplication in
	Substitution
is even	Definition of even
We see that if is even, then is also even is proven. Have proved

Paragraph proof do your proof in a paragraph.

You write a box at the end or smth.

Proof by Contraposition

goes to

Example 1:

Prove that if is an even and n is an integer, then n is even This proof is probably easier using the contrapositive

n is odd is odd This is the contrapositive

is odd

Not all full proof btw, just showing how you can use the contrapositive

Example 2

Actual proof Prove that if n = ab, where a and b are positive integers, then a ≤ √n or b ≤ √n.

We will be using a contrapositive n = ab dead end, so use cp

Scratch !( a ≤ √n or b ≤ √n) !(n = ab) (a √n and b √n) n != ab (ab b√n and b ) n != ab (ab b√n and b > n ) n != ab

Pf: I proceed by proving the contrapositive which states if a > and , then n != ab, for all a, b,

1		Premise
2		Premise
3		mult 1 by b
4		mult 2 by
5		simplify 4
6	ab > n	Transitivity on 3 & 5
7		def of >
Therefore, our proof by contrapositive suceeded, and thus, the equivalent “For all a, b , if n = ab then \leq\sqrt{n}$		b ” is true.

Proof by Contradiction

All props are either true or false When trying to prove p is true, assume that p is false. Given this, break some equality or property of mathematics. Thus, p is true.

We’d assume if p then q is false Giving us: Leading to (with simplification) is true

Example 1

Give a proof by contradiction of the theorem “If 5n + 2 is odd, then n is odd.”

In a proof by contradiction, assume is true, and find a contradiction.

Pf: I proceed using a proof by contradiction, where I assume 5n + 2 is odd, and n is even.

1	5n+2 is odd	premise
2	n is even	premise
3	n = 2k, for some k	def of even
4	5n = 10k	multi (3) by value of 5
5	5n + 2 = 10k + 2	add 2 to (4)
6	5n + 2 = 2(5k + 1)	factor (5)
7	5k + 1 = z, for z in	closure mult + add in z, meaning that multiplication and addition with integers, gives an integer
8	5n + 2 = 2z	sub (7) into (6)
9	5n + 2 is even	def. even
By (9) and (1), 5n+2 is both even and odd, which is a contradiction. Therefore, the original assumption that n is even is false, and “if 5n + 2 is odd, then n is odd” is proven.

Example 2

Show that at least four of any 22 days must fall on the same day of the week.

Scratch: Assume not p. At most, 3 of any 22 days must fall on the same day of the week. 3 * 7 = 21 Contradiction

Pf: Using proof by contradiction, I assume “At most, 3 of any 22 days must fall on the same day of the week”. Since there are 7 named days, and at most 3 fall on the same day, we have used at most 3x7=21 days, which contradicts that we have 22 days. Thus, our assumption was wrong, and at least 4 of any 22 days must feel on the same day of the week”

Example 3

Prove that √2 is irrational by giving a proof by contradiction Pf: I proceed using contradiction and assume We also note that a rational number can be written in simplest form. Thus, we have where , , and have no common factors , by squaring Thus is even, by closue prop. and def of even Since is even, p is also even. And p = 2k for some Then through sub, we have and thus, is even Thus q is even, and so q = 2m for some We see p and q both have a common factor of 2, which contradicts the premise that they had no common factors. Thus, our assumption that is ration is false, and we are left with as irrational.

Example 6

Let a and b be positive integers with the property that ab+1 divides a^2+b^2. Show that (a^2+b^2)/ (ab+1) is a perfect square.

Pf: Just watch the lecture, view the notes later

When to use direct vs indirect proofs

Simple suggestion: Just try it. Start with a direct proof and see what happens. Do scratch work. Never try to write a proof before doing scratch work. Longer suggestion: Hypotheses that can’t be easily reasoned from might suggest that you use an indirect proof. Look back to example 3.

Vacuous Proof, with , if , then the original statement must be true, regardless of q.

Trivial Proof with , whenever , then the original statement must be true, regardless of q.

Backwards Reasoning (Strategy) This is a strategy that you can use in your scratch work. 

• Suppose you’re proving that q is true from a list of givens.
• However, you’re unable to figure out where to start based on those givens.
• In this case, you might start with q and work backwards to something that you can prove using your givens.
• Then when you write up your formal proof, you can do all the steps backwards.

Example: Prove that (x+y)/2 > √(xy) for all distinct positive real numbers x,y

Scratch: Start assuming conclusion is true. Not equal, thus LHS will be gt0 Now for the Pf, just go backwards

Pf: Let , be arb. where . Then . Thus, * since the square of a nonzero real number is postive.

S	R
1)	By *
2)	Distr.
3)	Add 4xy
4)	Factor LHS
5)	sqrt 4)
6)	div by 2
We see that whenever x, y are distinct real # s, then

Exhaustive Proofs

In an exhaustive proof we try every possibility of the proposition. If all cases are true, then the proposition is proven.

e.g. Prove that if n is a positive integer with n ≤ 3.

Pf: I proceed by exhaustion Let Case: P(1)

Case: P(2)

Case: P(3)

By exhaustion, is true for all pos. int. where

Proof By Cases

A proof by cases is used when you must break your proof up into different cases due to a single argument not being enough to prove all cases. e.g. Prove that if n is an integer, then .

Pf: Assume is arbitrary. We have 3 cases: Case: Since , Case: since the square of an int is nonnegative. We know by transitivity, we have Case: Mult ineq by gives Since we have proven all cases, then the original statement is true.

Without Loss of Generality

Sometimes we can eliminate cases inproof when the cases are very similar. e.g. vs You can say WLOG because the proofs for these cases with be exactly the same, except the x’s and y’s with be flipped.

Induction

Let P(n) be a proposition. To prove P(n) for all integers k.

1. Basis step where we show P(1)
2. Inductive step where we show that if P(k) then P(k+1)

Ex: Prove that

Pf: Let P(n) be . I use inductionto show P(n) is true for all int. n >= 1.

Basis: P(1) is true bc

Inductive Hypothesis: Assume that is true for a fixed arbitrary integer

Inductive Step:

1 + 2 + … k
1 + 2 + … k + (k + 1)
""""
""""
""""
""""
We see that is true, completing the inductive step.
By math induction, P(n) is true for all int n >= 1

Make sure to add the term, not just k + 1

Let a be constant and r be a common ratio

Pf: Let P(n) be . We us math. ind. to prove P(n) for all in

Basis Step: P(0) is true because

Inductive Hypothesis: Assume

Inductive Step:

	IH
	add
	Summation def
	Simplify
	Distributive
	Simplify
	Commutative

Thus is proven, completing the inductive step. By induction, P(n) is true for all int.

Induction with Inequalities and Division

Use backwards reasoning in induction proofs in the SW to get the answer

~ Prove that people can divide the cake fairly.

n = 1 → whole cake n = 2 → 1/2 of whole cake n = 3 → 1/3 of each 1/2 n = 4 → 1/4 of each 1/3

Pf: Let be that people can divide a cake fairly, so that each person has of the cake. I use induction to prov is true for all integers

Basis: is true because one person would get the entire cake. 1/1

Inductive Hypothesis: Assume people can divide the cake equally into pieces where

Inductive Step: Consider people, by the inductive hypothesis, they split the cake such that each person has of the cake. Let another person join, now we have people. We will take of each existing person’s slice. In order words, they take of the original cake, from each of the original people. Since this occurred k times, they now have . Each of the original , originally had from which we took away . Meaning each other person also has of the original cake. Thus by math ind, ;

Strong Induction

Induction but you do You can also be like for domain such that

Set Theory

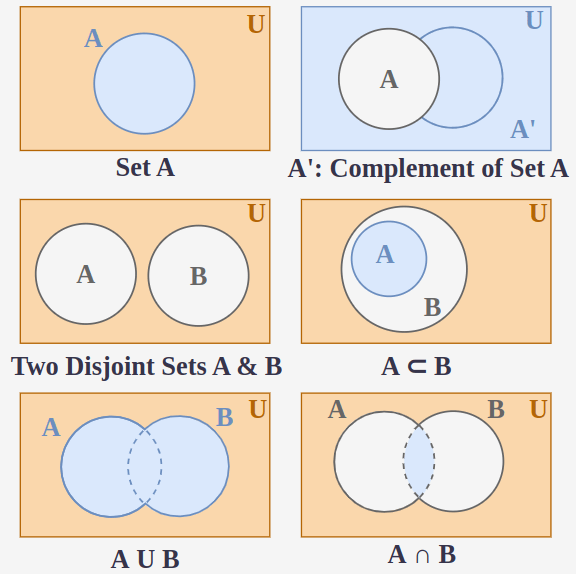
The study of Sets, which are collections of distinct objects.

Fundamentals

Transclude of Set

Subset

A part of a Set; Set A is a subset of B.

Definition

A set is a subset of if all elements of A are also elements of B.

Proper Subset

Link to original

Superset

A Set encompassing/extending another set; Set B is a subset of A.

• A superset is the converse of a Subset. They are defined the same way, but the operands are swapped.
• Exclusively using subsets is favored

Definition

Proper Superset

Link to original

Set Builder Notation

A set with some Object such that etc are true. e.g.

Link to original

Universe

The Universe, Universal Set, or Universe of Discourse, denoted by is the Set that contains all the entities one wishes to consider in a given situation.

• denoted mainly by but also sometimes by

Link to original

Venn Diagram

In Set Theory, a Venn Diagram is a diagram that visually demonstrates the relationship between Sets, their overlap, and their relation to the Universe of Discourse

Link to original

Principle of Inclusion-Exclusion

For 2 sets, for example

For 3 sets, for example Note that we add

Link to original

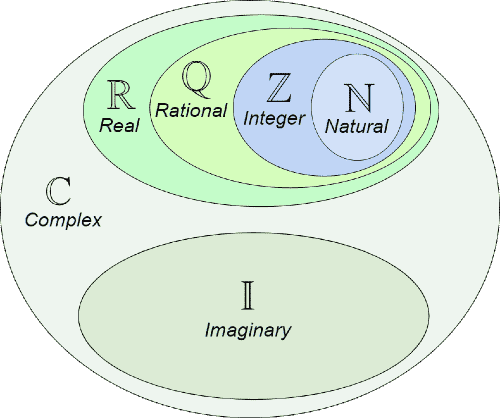
Numbers

Number

An element of a Division Ring, used for measuring, counting, quantifying, etc.

Set Name	Symbol	Description	Examples
Natural Number		Counting numbers
Whole Number	or	Nonzero Integers
Integer		Natural numbers, their negatives, and zero.
Rational Number		Any number expressible as a fraction .
Irrational Number		Numbers that cannot be fractions (non-repeating decimals).
Real Number		All points on the continuous number line ().
Imaginary Number
Complex Number
Quaternion
Octonion			Takes up too much space

Link to original

Functions

Transclude of Function

Domain

The Set of all inputs to a Function

Link to original

Codomain

The Set of all outputs of a Function

Link to original

Injective

If there is at most one location in the Codomain for every location in the Domain

Link to original

Surjective

If there is a location in the Codomain for every location in the Domain

Link to original

Bijective

If there is exactly one location in the Codomain for every location in the Domain for the Transformation

Link to original

Link to original

Functions

• Definition 1: Let A and B be nonempty sets. A function f from A to B is an assignment of exactly one element of B to each element of A. We write f (a) = b if b is the unique element of B assigned by the function f to the element a of A. If f is a function from A to B, we write f : A → B.
• Definition 2: If f is a function from A to B, we say that A is the domain of f and B is the codomain of f. If f (a) = b, we say that b is the image of a and a is a preimage of b. The range, or image, of f is the set of all images of elements of A. Also, if f is a function from A to B, we say that f maps A to B.
• You must specify the domain, codomain and the mapping of elements of the domain to elements in the codomain when defining a function. The range does not need to be explicitly specified
• Two functions are equal when they have the same domain, codomain, and map each element of their common domain to the same element in their common domain.
  • Changing the domain, codomain or mapping creates a new function

Ex:

1. What is the domain, codomain, and range of a function that assigns the last two bits of a bit string of length 2 or greater to that string.  (E.g. f(11010) = 10)

• Domain
  • The set of all bit strings 2
• Codomain
  • {11, 01, 10, 00}
• Range
  • {11, 01, 10, 00} Range and Codomain here happen to be equal

2. Let f : R→ R assign the square of a real number to this real number. Then, f (x) = .. What is the domain, codomain, and range of f.

• Domain
• Codomain
• Range
  • set operators have to order of precedence, except with union, intersect, and remove

1. ()
2. ~ complement
3. Everything else left to right

Real-valued and Integer-Valued

• A function is called real-valued if its codomain is the set of real numbers
• it is called integer-valued if its codomain is the set of integers.
• You can add and multiply both real-valued and integer-valued functions

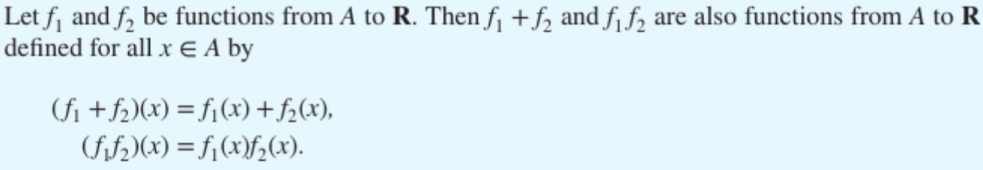A not necessarily a set of numbers

Ex

Let f1 and f2 be functions from R to R such that f1 (x) = x2 and f2 (x) = x − x2 . What are the functions f1 + f2 and f1 f2 ?

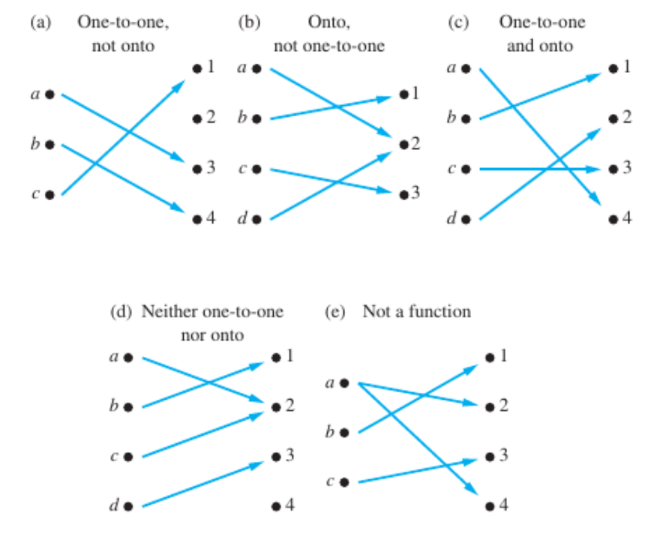
One-to-One Functions

Some functions never assign the same value to two different domain elements. These functions are said to be one-to-one.

• At most one mapping from the domain for every element of the codomain
• Note that a function f is one-to-one if and only if f (a) ≠ f (b) whenever a ≠ b, and vice versa.
• Note 2 in the codomain below

Example: Determine whether the function f (x) = x2 from the set of integers to the set of integers is one-to-one.

• False, every value square is also hit by its opposite squared
• Assume domain if not given, to be the most reasonable real numbered domain or something similar.

Example: Prove that the function f (x) = x + 1 from the set of real numbers to itself is one-to-one.

• You need to show that if f(a) = f(b), then a = b By inspection it is 1-1 because it just shifts any value in the domain up by one. f: R→R Pf: Let a,b be arbitrary and assume f(a) f(b). Then by def of f(x): a + 1 = b+1 a=b Since f(a)=f(b) → a=b f(x) is 1-1, by definition

A function has to map all element in the domain to something in the codomain. Let the domain be R, the codomain be R. then f(x) = 1/x is not a function.

Increasing and Decreasing

Given , and x, y are in the proper domains, f is called:

• increasing if f (x) ≤ f (y)
• strictly increasing if f (x) < f (y)
• decreasing if f (x) ≥ f (y)
• strictly decreasing if    f (x) > f (y)

Its defined exactly as what you’d think it would mean. Not all function match. Horizontal line would be both. Vertical line would be neither.

Example: show that    from R+ to R+ is strictly increasing. let x, y be positive reals and

Onto Functions

A function f from A to B is called onto, or a surjection, if and only if for every element b ∈ B there is an element a ∈ A with f (a) = b. A function f is called surjective if it is onto.

• The range of the function equals the codomain. (every element in codomain is used.)
• All elements of codomain are hit at least once
• range = codomain

Let f be the function from {a, b, c, d} to {1, 2, 3} defined by f (a) = 3, f (b) = 2, f (c) = 1, and f (d) = 3. Is f an onto function? Yes.

Is the function f (x) = from the set of integers to the set of integers onto? No. Not onto. All non square integers will be missed from the codomain. For example: 2,

Is f (x) = x + 1 from the set of integers to the set of integers onto?

• Consider an arbitrary element y ∈ B and find an element x ∈ A such that f (x) = y. Let y in Z (codomain). Try to find x in the domain that makes x+1=y. x = y-1 ← Guaranteed to be in domain? (Yes for this case bc closure).

Bijections

The function f is a one-to-one correspondence, or a bijection, if it is both one-to-one and onto. We also say that such a function is bijective. Exactly one domain element for every codomain element.

• Bijections have special properties
• All bijections have an inverse function

Inverse

Let f be a one-to-one correspondence from the set A to the set B. The inverse function of f is the function that assigns to an element b belonging to B the unique element a in A such that f (a) = b. The inverse function of f is denoted by f −1 . Hence, f −1(b) = a when f (a) = b.

Let f : Z → Z be such that f (x) = x + 1. Is f invertible, and if it is, what is its inverse? f(x) is a bijection f(x) is invertible

Get inverse. Replace f(x) with x. Replace x with

Let f be the function from R to R with f (x) = . Is f invertible? f(x) not a bijection

Composition of Functions

Let g be a function from the set A to the set B and let f be a function from the set B to the set C. The composition of the functions f and g, denoted for all a ∈ A by f ◦g, is the function from A to C defined by (f ◦ g)(a) = f (g(a)).

Let g be the function from the set {a, b, c} to itself such that g(a) = b, g(b) = c, and g(c) = a. Let f be the function from the set {a, b, c} to the set {1, 2, 3} such that   f (a) = 3, f (b) = 2, and f (c) = 1.  What is the composition of f and g, and what is the composition of g and f ? a → 3, c→1,b→2 a→undefined; g(f(x)) undefined, so the composition does not exist

Let f and g be the functions from the set of integers to the set of integers defined by f (x) = 2x + 3 and g(x) = 3x + 2. What is the composition of f and g? What is the composition of g and f ?

, but it is possible, just in general

Floor and Ceiling Functions

Floor

largest integer less than or equal to

Ceiling

smallest number greater than or equal to

Big-O Notation

Definition

Memorize: C and k are called witnesses to the relationship f(x) is O(g(x)).

• Trying to find an upper bound estimate of our function, i.e. if is a quadratic, its big O is
  • In this class, not trying to find smallest upper bound, unlike in computing
  • We are just finding an upper bound
• k for when g(x) is growing faster than f(x) and is than f(x)
  • k doesn’t need to be the first x where this occurs, just one of them
• What C means is that we only care about the parent function, i.e. we consider if then where , so that the functions are comparable.

Pf: show that is I proceed directly. (This proof only works for polynomials) Prove each term is

Did not have to pick this value, its just easier Thus C=4, k=1 as witnesses: is

Big-O Complexity

Have to memorize the theorem numbers.

Cardinality of Sets

Equal sets

Two sets A and B have the same cardinality if and only if you can find a bijection from A to B. When A and B have the same cardinality, we write |A| = |B|

Different Sets

If there is only a one-to-one function from A to B, the cardinality of A is less than or the same as the cardinality of B and we write |A| ≤ |B|. Furthermore, if there is a one-to-one function from A to B but there is no bijection, then |A| < |B|

Countable

• Finite sets are countable
• The set of positive integers is countable
• Any infinite set that has the same cardinality as the set of of positive integers is countable.
• When an infinite set S is countable, we denote cardinality of S by (read as aleph null). |S| =

Hilbert’s Grand Hotel

Consider a hotel with a finite number of rooms.  Suppose all rooms are occupied. A new guest arrives.  Then there is no way to accommodate this guest without evicting a current guest.

Hilbert’s Grand Hotel: Consider a hotel with an infinitely countable number of rooms.  Assume all rooms are occupied. Suppose a new guest arrives.  Show that this guest can always be accommodated. In other words, show that we can always find a room for this guest without evicting a current guest.

Cantor’s Diagonalization Technique

The one that proves is countable with the diagonals

Uncountable Sets

Show that the set of real numbers is uncountable. Hint: Show that (0,1) as a subset of R is uncountable which would show R is also uncountable

Division

Modular Arithmetic

Integer Representation

Base Conversion

Note: on exam, must use base conversion algorithm, not guess and check.

Prime