Graph

A nonlinear Data Structure which consists of a set of vertices (nodes) connected by edges where the edges may be directed or undirected.

• If the same vertices are connected in the same way by edges, the graphs are the same; it doesn’t matter how you draw the graph so long as it satifies the aforementioned condition

Examples	Vertices	Edges
Maps	Cities	Roads
Computer Architecture	Components	Bus
Neural Network	Neuron	Synapse
Social Media	Users	Relation
Internet	Computers/Servers	Telecom Infrastructure

Terminology

• Vertex
• Edge
• Order
• Size
• Adjacent
• Connected
• Incident
• Dense
• Sparse
• Simple
• Cyclic
• Degree
• Directed
• Path
• Trail
• Walk
• Circuit
• Weight

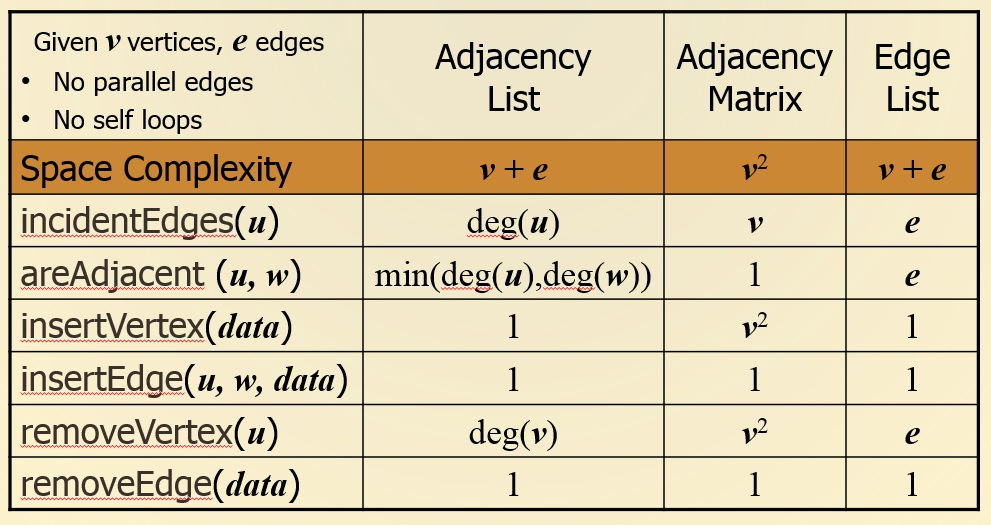
Graph ADT Methods

• vertices() returns iteration of all vertices
• edges() returns iteration of all edges
• numVertices() returns count of all vertices
• numEdges() returns count of all edges
• endVertices(e: Edge) returns endpoint vertices of given edge
• getEdge(u: Vertex, v: Vertex) returns edge from u to v or else null
• numEdges(v: Vertex) returns iteration of all outgoing edges to v
• opposite(v: Vertex, e: Edge) returns the other vertexx u that is incident to v for edge e
• insertVertex(d: Value) create a return new vertex with value d
• insertEdge(u: Vertex, v: Vertex, e: Edge) create a return new Edge e from vertex u to v
• removeVertex(v: Vertex) removes vertex v and all incident edges for v from the graph
• removeEdge(e: Edge) removes edge e from the graph

Graph Representation Data Structures

Adjacency Matrix

Like a stochastic matrix. Undirected graphs always result in symmetrical matrices. Rows are coming out of that vertex, Columns are arriving at that vertex 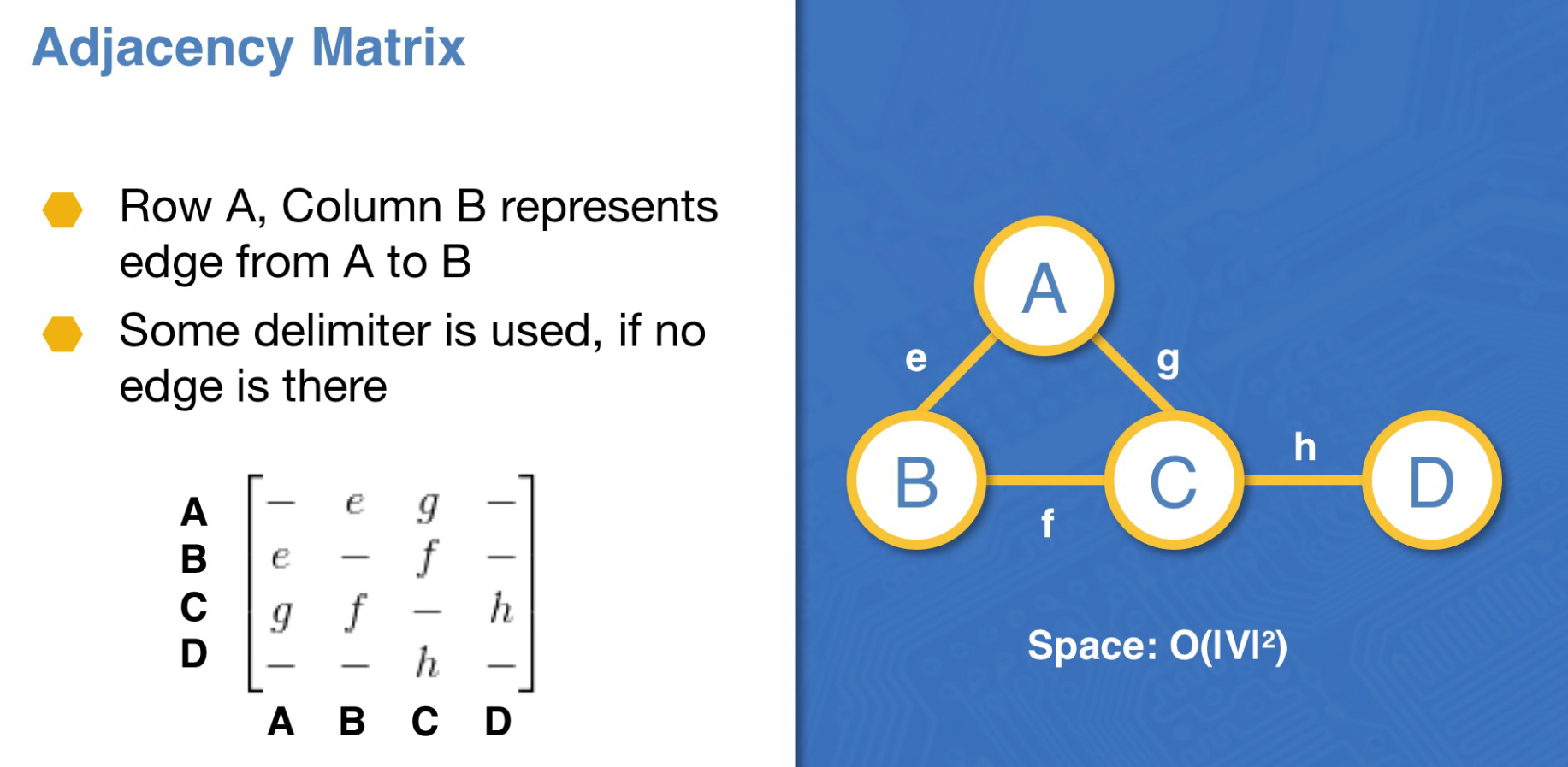Works well for a dense graph. Works well if you need to represent weights. Does not work well for adding vertices because you have to copy everything over.

Adjacency List

HashMap with external chaining where the size of the map is the size of the graph. 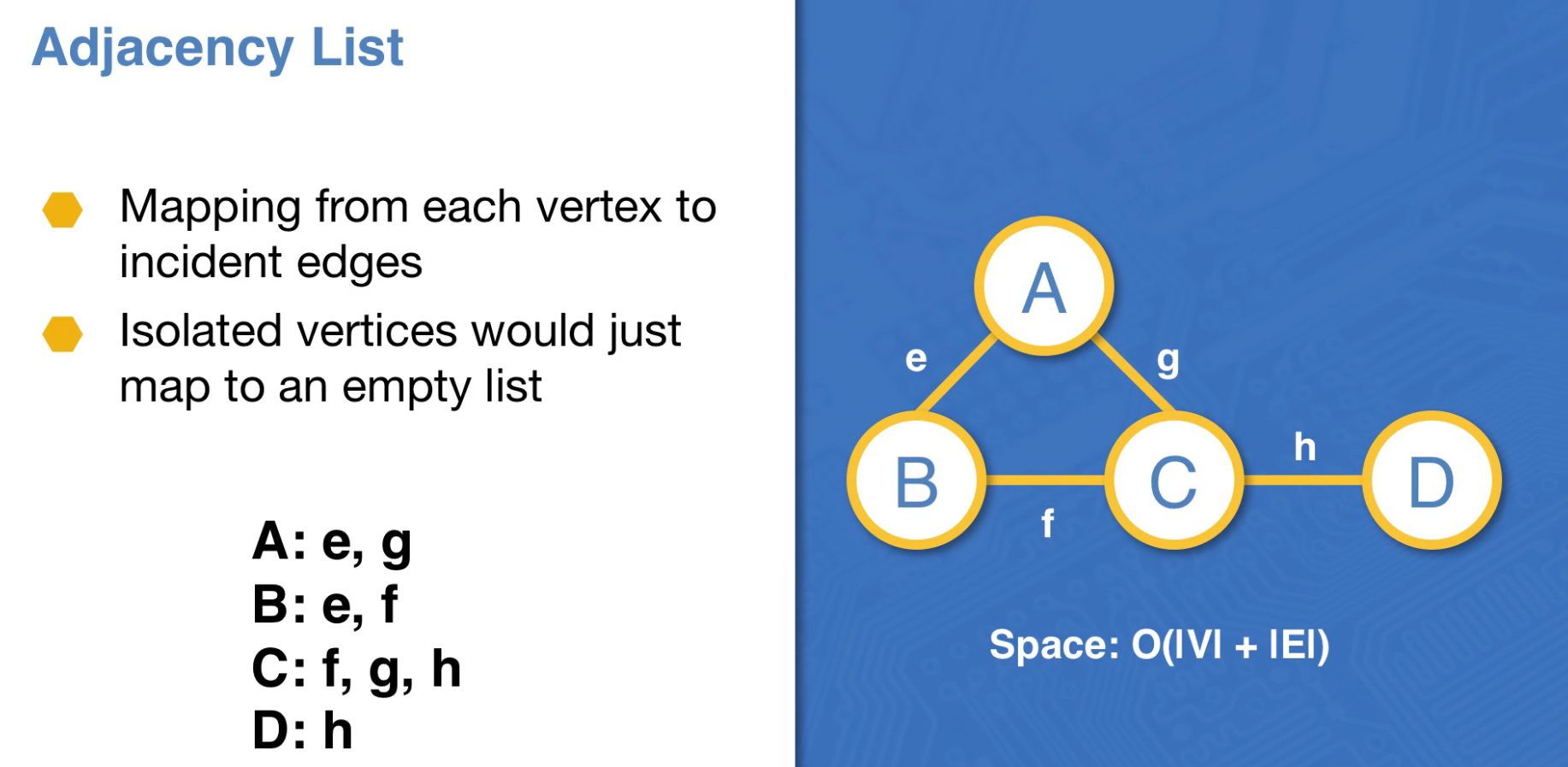Works well when the graph is sparse.

Edge List

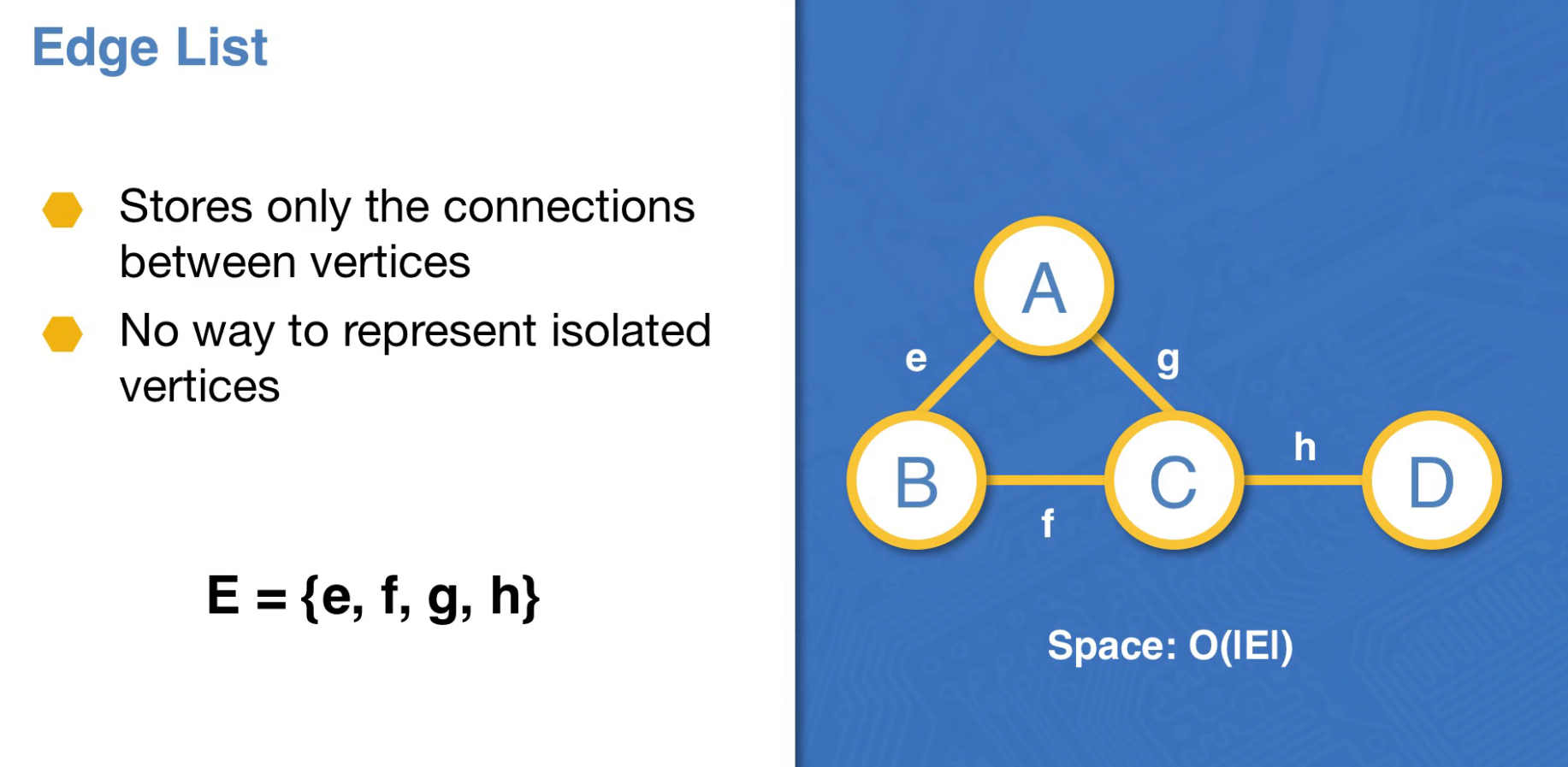Doesn’t work for disconnected vertices.

Variations

• Tree
  • Spanning Tree
    • Minimum Spanning Tree
  • Binary Tree
    • Binary Search Tree
  • AVL
  • 2-4 Tree
• Linked List
  • Singly Linked List
  • Doubly Linked List
  • Circular Singly Linked List
  • Stack
  • Queue
  • Deque
• SkipList

Efficiency

See also

Traversal Algorithm