2-4 Tree

• Kind of Tree where every node must have 2-4 children, and 1-3 data values.
• Guarantees operations through Balancing Scheme
• Structure
  • 2-4 Children
  • 1-3 data values
  • m data values have m + 1 children, and vice versa
  • Nodes grow and shrink with the data
• Shape > Order > Node
• Data always gets put into a leaf initially when added
• When promotion occurs in a node with 3 siblings, promote the value as normally, and split as normally. There will temporarily be 4 data in the parent and 5 children. This will be resolved by the enforcement of balancing scheme, as the parent node will also promote. The overflow will be promoted up the tree in general until resolution.
• When fusion happens with a parent of one value, there will temporarily be a node with 0 values and children.

Balancing Scheme

TLDR:

• All leaves must have same depth
• All Nodes must have 2-4 children
• All Node must have 1-3 data values.

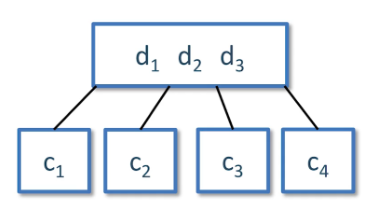
Shape Property

All leaves must have same depth

Order Property

Node Property

is the nth value is the nth child Each node must have 1-3 data Each node must have 2-4 children

Adding

Similar to other Tree adding methods, adding is simpler than removing

Overflow

• Recall that every node must have 1 - 3 data. If we add more than this, we enter overflow. In order to resolve overflow with me “promote” one of the middle nodes. This node is either the second or third node, and the choice is arbitrary.
• When a promotion occurs
  • The promoted value is moved upwards
    • Either into the node above it
    • Into a new root if being promoted from the current root
  • The overflowed node is “split” while maintaining the Order Property.

Removing

• Remove the data
• If the node is an internal node, replace it with its Predeccesor/Successor. If you remove from a Leaf without Underflowing it, that’s all! 🙂

Underflow

When removing, we may get a node with 0 values. This is called underflow and it is resolved by Transfer and Fusion.

• A transfer is preferrable over a fusion, because fusion may propagate underflow up the tree.
• If you propogate underflow up to the root, it gets deleted.

Transfer

Transfer between parent and child. In either direction. Applicable if the node we are stealing from has multiple data.

Parent to Child

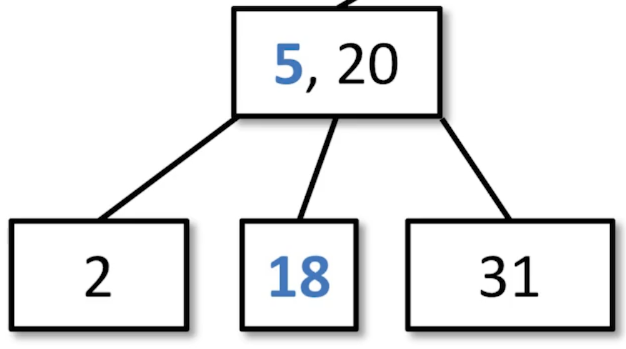
Replace with Predeccesor/Successor. 18 replaces 12. This is because 12 is an internal node. This is not specific to transfer.

This child node is underflowed, so we need to steal from the parent. Check the adjacent siblings of the node for more than 1 value. If there is one that satisfies this, move that data into the parent, pushing the value in front of it into the empty node.

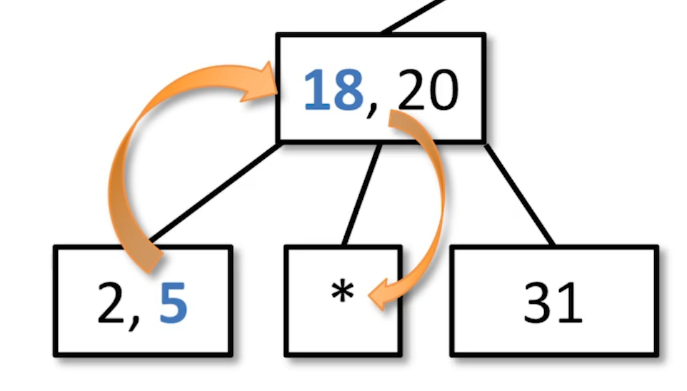
Child to Parent

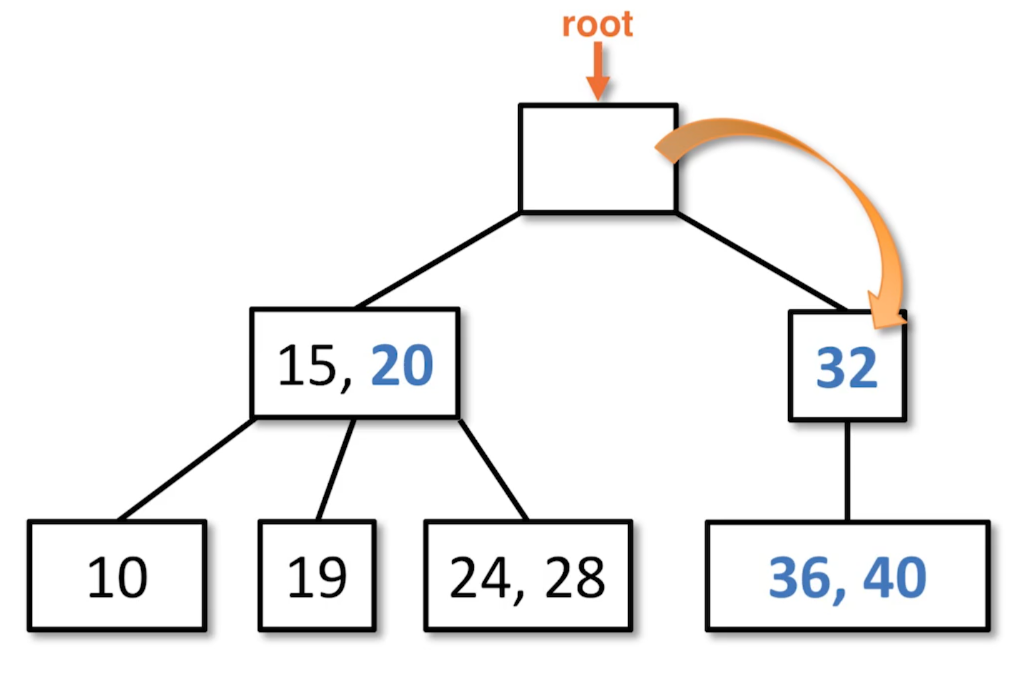
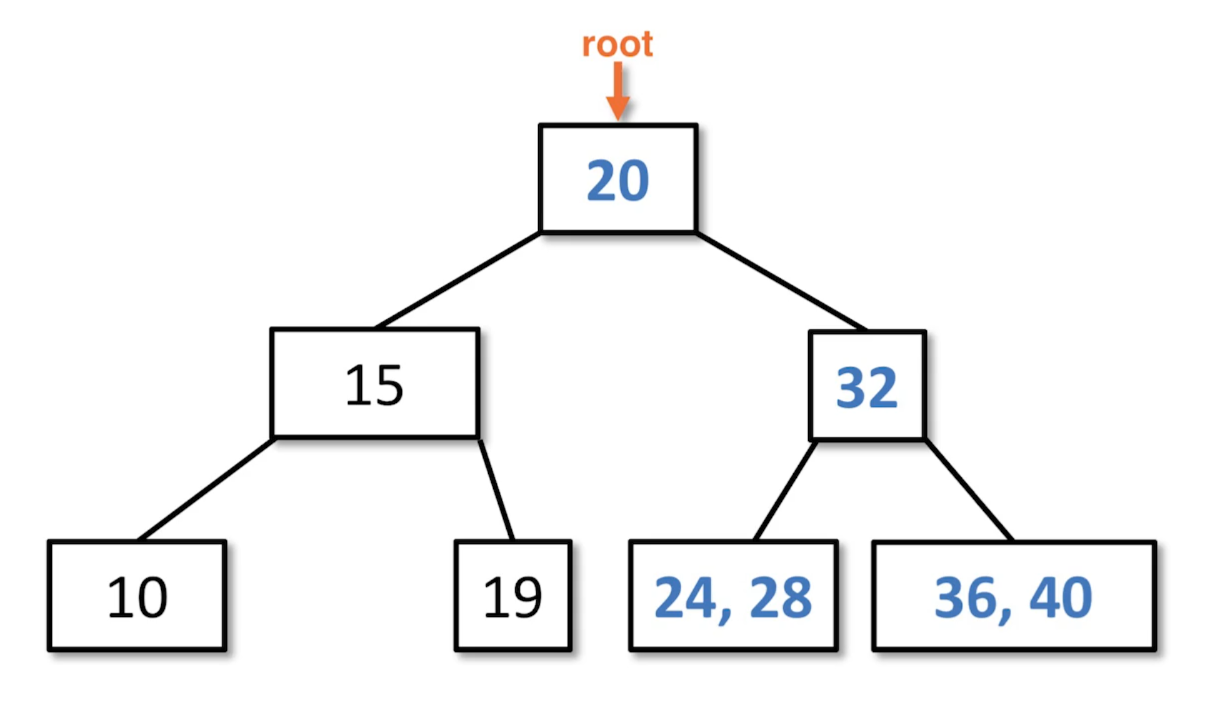
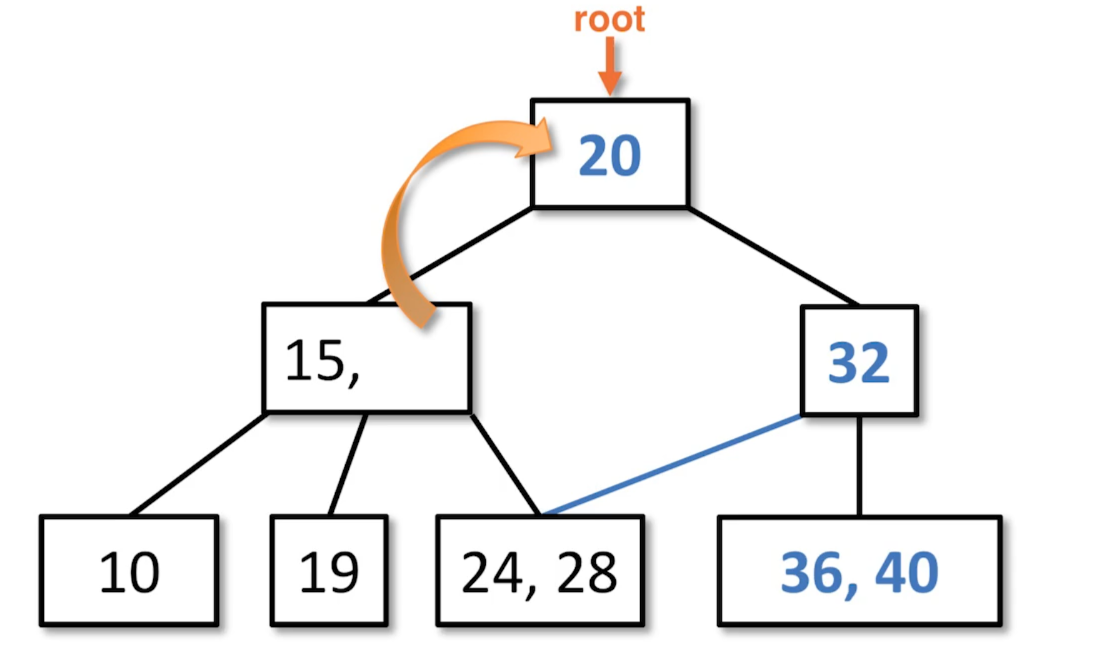
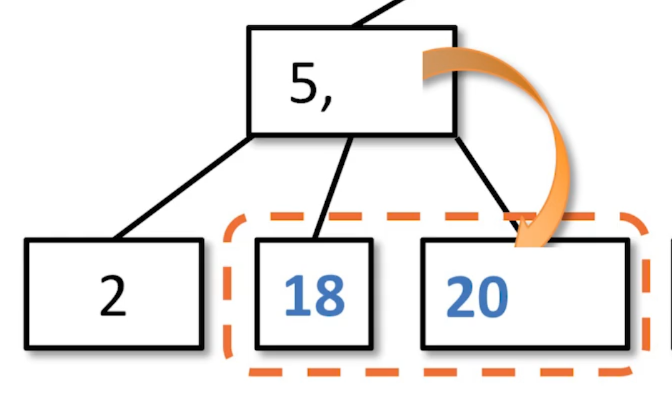
We are in the process of balancing this 2-4 tree. There was some underflow that originated on the right side that propogated all the way up the tree.

The root is underflowed, so we steal from one of the children, because the left child has two values. 20 is the closest value.

In order to enforce the Order Property, the 2428 node is moved while maintaining the property.

Fusion

Fusion between siblings with single data. When Transfer is not an option.

Example

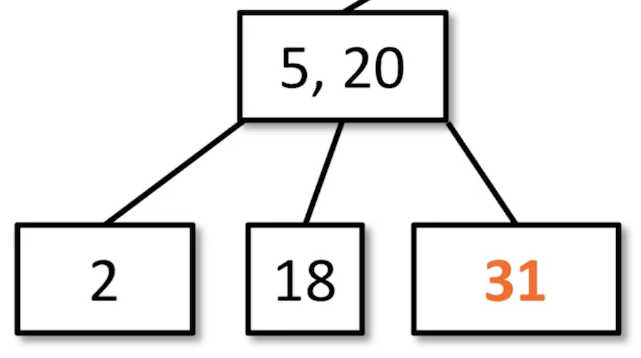
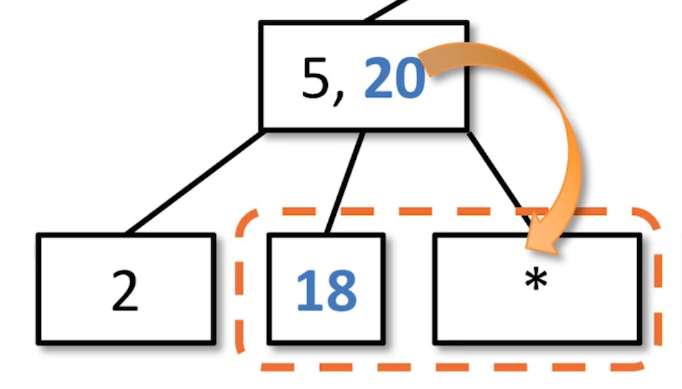
Check for Transfer. It is not possible in this case because the siblings only have 1 value each.

Bring down the closest data value into the underflowed node.

Fuse the data that was brought down from the parent and its neighboring sibling.

Flowchart