Self balancing Binary Search Tree used to eliminate O(n) worst case
- The tree must be Balanced, |balancefactor| ⇐ 1
- calculate height and balance factorr from the leaves up/bottom up
- Node height and balance factor are stored inside each node where
- height = max(height(left), height(right)) + 1
- balancefactor = height(left) - height(right)
- Balance factor tells us if a node is right or left heavy, i.e. if it has more nodes in its right or left subtree. We want these counts to be similar if not equal, in order to maintain logarithmic time complexity.
- Add in level order of apparent graph order to recreate
Rotations
To restore balance in an AVL
If Parent and child BF match, the it’s a single rotation, otherwise its a double rotation.
In all cases the B node gives its left subtree to the tree to the left of it, and its right tree to the right of it. The B node becomes the parent node of the side nodes. The B node is the middle node, from a vertical perspective. It is actually the middle for single rotations, and it is the bottom node for double rotations.

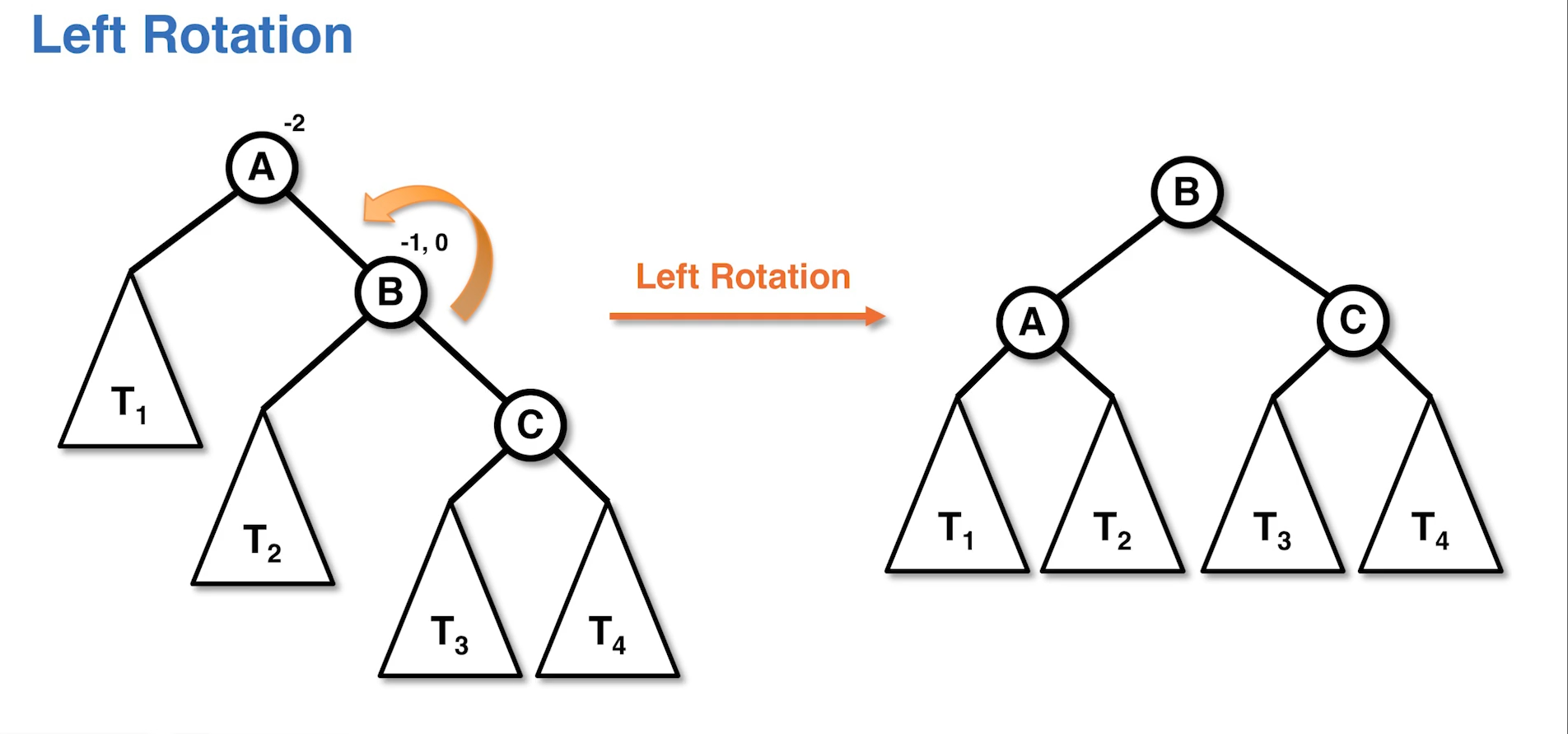
Left Rotation
Node BF < -1, Right BF = -1, 0
Right Becomes parent, gives subtree to node
Right Rotation
Node BF > 1, Left BF = 1, 0
Left Becomes parent, gives subtree to node

Right-Left Rotation
Node BF < -1, Right BF = 1
Right Rotation on C, then Left Rotation on A

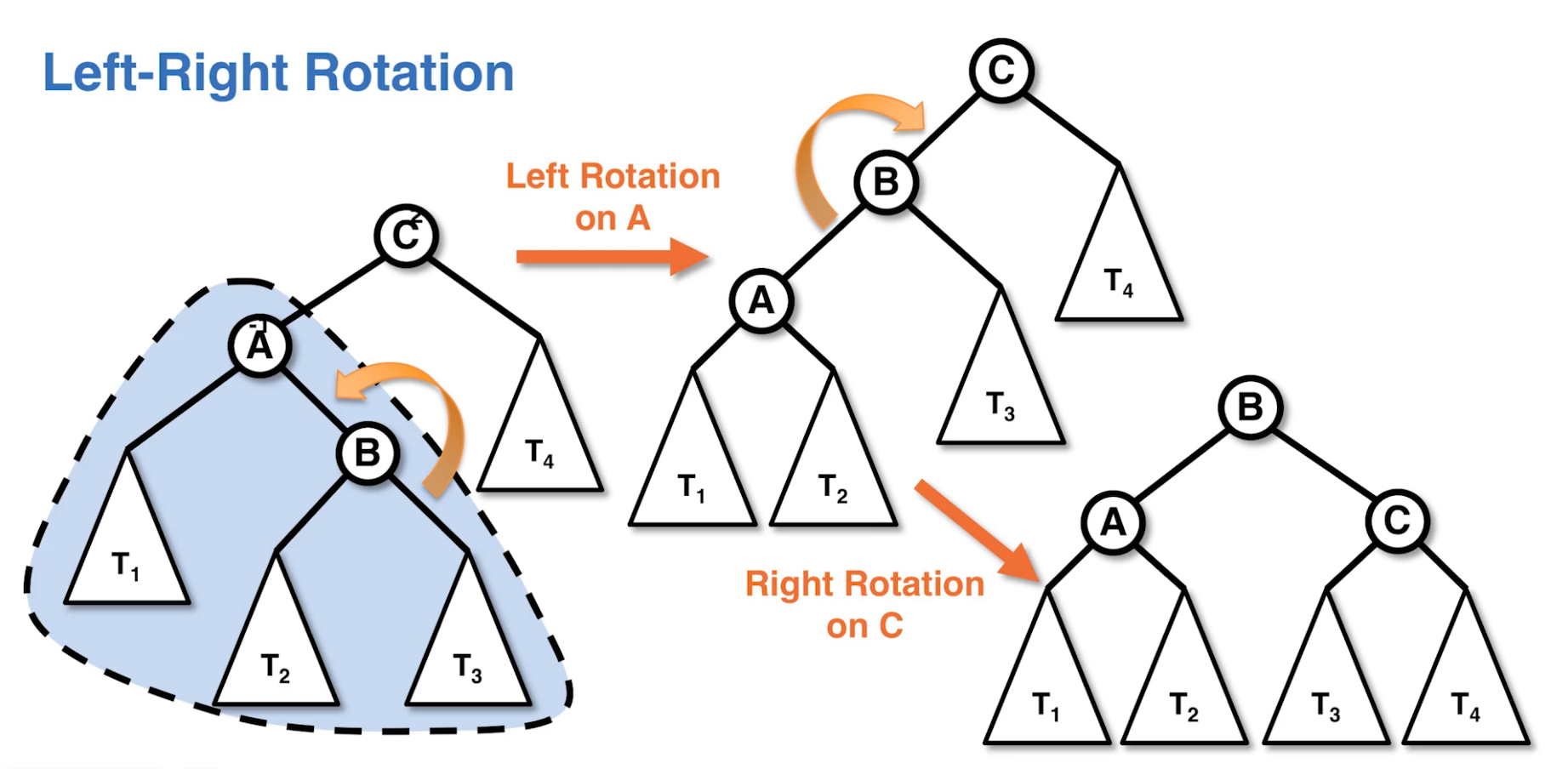
Left-Right Rotation
Node BF > 1, Left BF = -1
Left Rotation on A, then Right Rotation on C