Lorentz Transformation

A modification of Galilean Transformations which accounts for Special Relativity

Implies that ordering of events depends on the observer

Time Dilation vs Length Contraction

1. Why is a reference frame that is moving relative to a stationary observer Dilated (multiplied) by for time, but contracted (divided) by for length?

   Each measurement involves its own special conditions.

   • Time
     • Must use Lorentz Transformation
   • Length
     • • (really they could be anything, but they don’t strictly need to be equal)
     • Must use Inverse Lorentz Transformation

2. Related? Due to the symmetrical nature of Special Relativity, from one frame, there is Time Dilation, but from the other there is Length Contraction. Therefore, they are two ways of describing the same effect

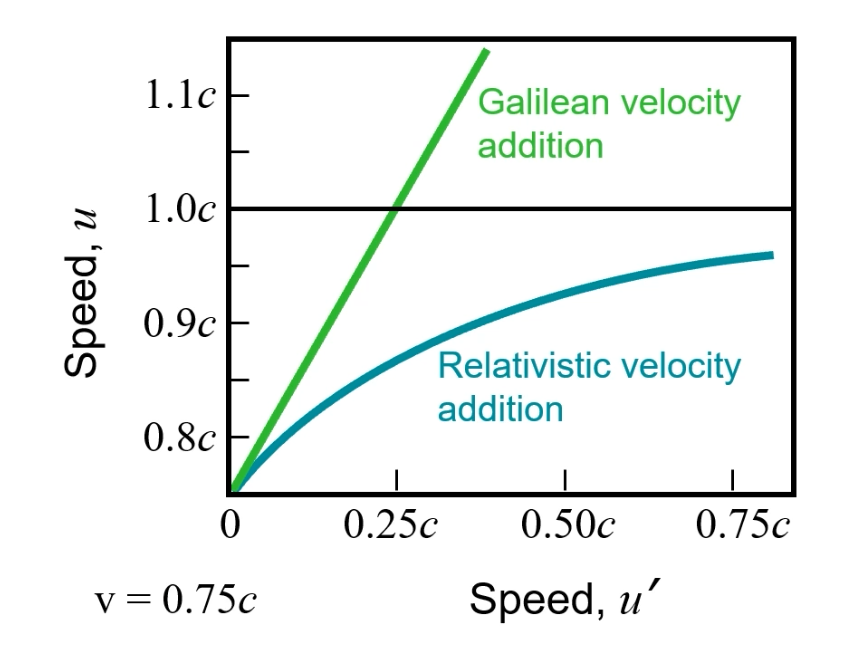
Relativistic Velocity Addition

Note that it’s impossible to achieve the Speed of Light See Star Trek reference in Special Relativity Lecture No. 2

• Particle interactions that emit Photons do not affect the speed of the photons, which is constant at the Speed of Light
• 

See Also

Time Dilation Length Contraction