Least Squares

Given

Given many data points, construct a matrix equation in the form of a linear equation (this matrix equation will be overdetermined). The matrix equation below is This equation is linear but it doesn’t have to be, just adjust accordingly to represent the equations as a matrix equation.

Goal

Using Best Approximation, find a vector in subspace closest to

is a subspace of , , i.e. Note: Can only use Orthogonal Decomposition for when the columns of A form an orthogonal basis, by definition

In other words, is closest vector in to Note: is a unique vector, a special that minimizes the above equation. Note: If the columns of are orthogonal, then you can just use the scalar projection of onto each column of .

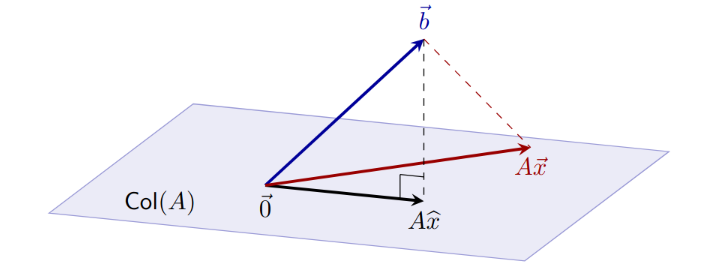
Normal Equations

The least squares solutions to corresponds to the solution to

• Turns the equation from above and transforms it into a square matrix equation

Derivation

• is the Least Squares Solution to

Normal Equation Usage

• Use when non-square matrix
  • Over/Under determined
• Regression

Theorem (Unique Solutions for Least Squares)

If A is m x n

• Ax = b has a unique least squares solution for each b in Rm
• Cols of A are linearly independent
• The matrix A^T A is invertible If the above hold, the unique least square solution is

If the above conditions are not true, there may be infinitely many solutions, or some other nonunique amount of solutions, in which case you should consider instead.

Note: plays the role of the “length squared” of the matrix A

Theorem (Least Squares and QR)

Examples

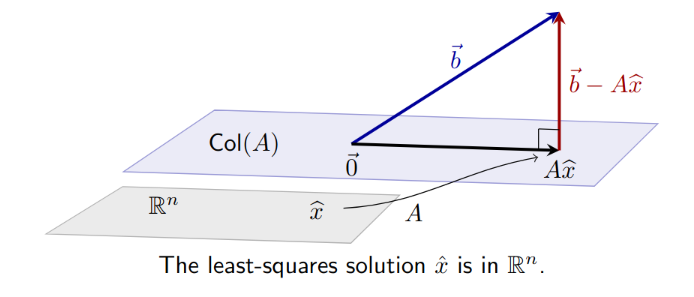
Hampton Explanation for Least Squares

Let . is the unique, minimizing solution to the equation such that

• Essentially, minimize
  • is the minimal distance between the different solutions
• Goal: Find s.t. is closest to
• in this context just denotes the special/unique that minimizes the distances between and b is closer to Axhat than to Ax for all other x in Col A
• If b in Col A, then xhat is…
• Seek so that is as close to as possible, i.e. should solve Axhat = bhat