General Relativity

A generalization of Special Relativity that expands it to non-Inertial Reference Frames, i.e. accelerated frames. The idea that Gravity bends Spacetime, acceleration and gravity are indistinguishable.

Principle of Equivalence

Inertial Mass

Intertial mass measures how strongly an object resists a change in its motion

Gravitational Mass

Gravitational mass measures how strongly an object attracts and is attracted by other objects

Realization

Combining the two equations

In order to say that the acceleration is equal , both masses must be equivalent. This equivalence is important, as the resistance to change in motion and the attraction to other bodies aren’t obviously related. Consider the experience of a person on the surface of the earth. They experience an acceleration of into the ground. They drop an object and it falls to the floor, accelerating at . Consider the experience of a person in a rocket in space, accelerating at . They experience an acceleration of into the floor of the rocket. They drop an object and it falls to the floor, accelerating at . A person cannot tell the difference between the two situation. There is no experiemnt that can be done in a small confined space that can detect the difference between a uniform gravitational field and an equivalent uniform acceleration Therefore, acceleration and gravitation are indistinguishable.

Curvature of Spacetime

The modeling of the above effects as to the curvature of Spacetime, due to matter.

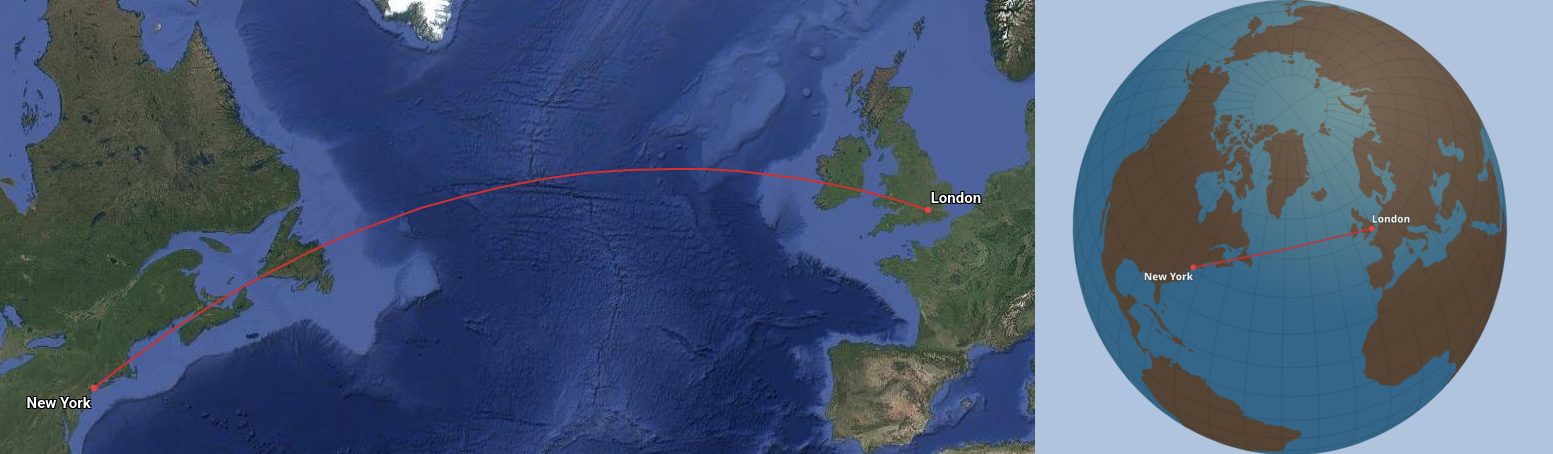
Light, for example, travels straight from its frame. However, because spacetime may be curved, this straight line would also be curved. See https://en.wikipedia.org/wiki/Geodesic A good example of visualizing what this could look like is: imagine a commerical flight traveling from New York to London. Ignore currents in the earth’s atmosphere. In order to minimize costs, we want to fly in a straight line directly from one city to another. However, because our space is curved, on account of being spherical, the path is not straight in the layman sense, but it minimizes the path length between the two points on the globe so it is by definition a straight line.

Consequences

Light Bending

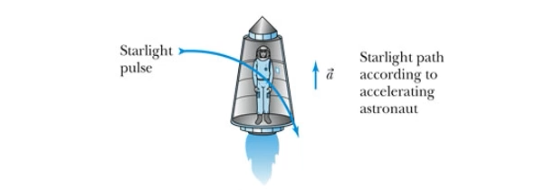
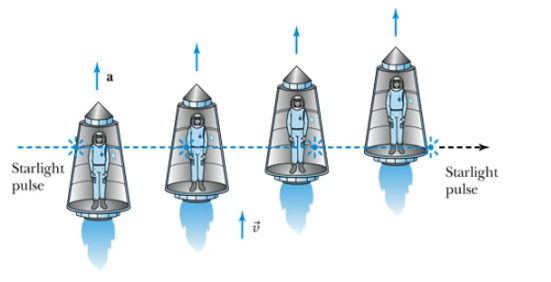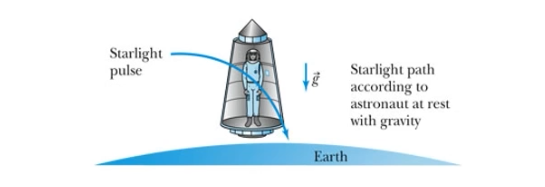
Consider traveling in a spaceship at acceleration where gravity is negligible. There is some incident light. This light takes time to travel, so it will pass the closer side of the ship higher than the farther side of the ship. From the accelerated frame, the light apparently curves down. The Principle of Equivalence implies that at rest on Earth, the light must also bend downward in this way.

Gravitational Doppler Effect

Principle of Equivalence implies a Doppler shift of light, proportional to Earth’s gravity. A light pulse shone vertically upward will lose energy as it travels up, just as a rock thrown up would, due to gravity. Because (Planck’s Radiation Law), the frequency of the light is shifted due to gravity. Light shone towards the Earth is blue-shifted, and light shone away from the earth is red-shifted. In the case of a typical rock being thrown, it will probably not reach escape velocity, while light generally will. However, the case of light failing to reach espace velocity would be that of a Black Hole. See Schwarzschild Radius

Spacetime Metric

For Special Relativity first By Einstein Notation, there is implicit summation over the whole range

For General Relativity

Eistein Tensor

See Ricci Tensor, Christoffel Symbol

Einstein’s Field Equations

Correspondence Principle

Einstein’s Field Equations reduce to Newton’s Law of Gravity in the weak-field and slow-motion limit.

See also

Event Horizon Critical Density Einstein’s Field Equations Inertial Reference Frame