Prim's Algorithm

A Minimum Spanning Tree Algorithm

• Greedy Algorithm
• Very similar to Dijkstra’s Algorithm as it is looking for the shortest Weight from one vertex to its Adjacent vertices.
  • Both of them
    • Have start vertex
    • Store seen vertices in minHeap
    • At each step mark a vertex as visited, and add its neighbors to heap
  • Dijkstra’s
    • assigns priority based on distance from start vertex
    • returns a shortest path
  • Prim’s
    • assigns priority based on distance from current node to the next greedy vertex
    • returns a Minimum Spanning Tree
• Focuses on Connected Graphs
• Builds the Minimum Spanning Tree one Vertex at a time
• If a graph is not connected, what is generated is a Minimum Spanning Forest
• Vistool

More Info - Graph Cut

Let’s address the Graph Cut property. Conceptually, the algorithm refers to a cut property across the edges in a graph. The cut property of MSTs states that any MST must include the minimum cost edge over any graph cut . The entire basis for why Prim’s algorithm works is this property! Prim’s algorithm maintains a set of visited vertices, which are the vertices connected by the MST at that specific point in the progression of the algorithm. 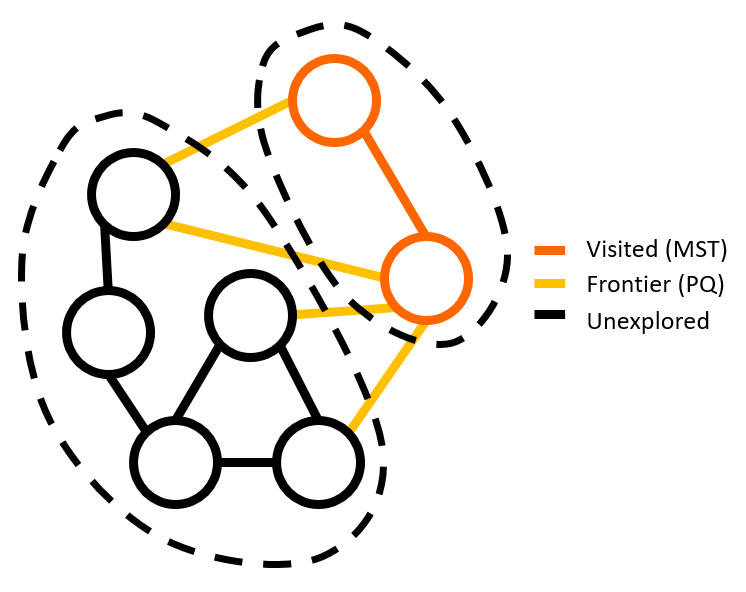This visited set implicitly creates a graph cut between visited vertices and unvisited vertices. The edges in the priority queue (the “frontier” is what we called it in Dijkstra’s) are precisely the edges in this graph cut, and the priority queue will of course give us the minimum cost edge.

Efficiency

for the same reasons as Dijkstra’s Algorithm

• If the graph is Dense, then
• If the graph is Sparse, then

Implementation

• Visited Set to track where we have been
• Heap of Edges with shortest distance to another vertex
  • The next edge in the heap represents the shortest edge to take next
• Edges of minimum Weight that are traversed are stored in an MST Edge Set
• for all neighbors of Edge(u, w) not in VS is the same as saying for all edges leaving the Graph Cut

prims(start: Vertex) {
	VS: Set<Vertex>, MST: Set<Edge>, h: minHeap<Edge>
	VS.add(start), h.add(start.edges)
	
	while (h and VS < G) {
		edge(from: Vertex, to: Vertex) = h.poll()
		if (to !in VS) {
			VS.add(to)
			MST.add( edge(from, to) )
			for to.edges: edge(to, x) st x not in VS {
				h.add(edge(to, x))
			}
		}
	}

	return MST < 2*(V - 1) ? null : MST
}