Merge Sort

Recursively split the array into subarrays until each subarray is sorted (one element). Join the subarrays back together into sorted subarrays until the final sorted subarray is the original dataset in sorted order.

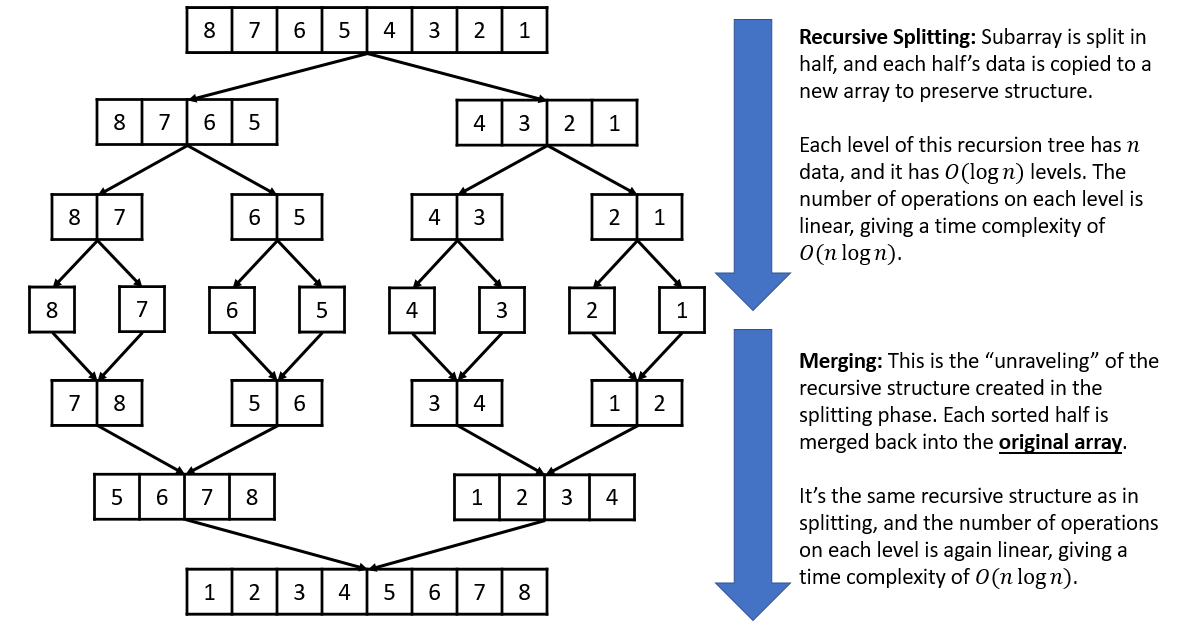
Memory intensive solution. Should not be used in cases where memory is scarce or slow.

Evaluation

	Best Case	Average Case	Worst Case	Stable	Adaptive	In-place
Merge Sort				Yes	No	No

Pseudocode

merge(array) {
	if array.length <= 1 -> return

	// Recursively bisect array
	left = array[ ... length / 2 - 1]
	right = array[length / 2 ... ]
	merge(left)
	merge(right)

	// merge sorted subarrays into larger subarray
	i := 0 (index of left subarray)
	j := 0 (index of right subarray)
	while i, j not at end of left and right arrays, respectively {
		if left[i] <= right[j] {
			array[i + j] := left[i]
			i++
		} else {
			array[i + j] := right[j]
			j++
		}
	}

	// in the case that the right elements were all already copied
	// empty remaining left elements into larger subarray
	while i < left.length {
		array[i + j] := left[i]
		i++
	}
	// in the case that the left elements were all already copied
	// empty remaining right elements into larger subarray
	while j < right.length {
		array[i + j] := right[j]
		j++
	}
}

See also

Sorting Algorithms