Orthogonal Decomposition

I proceed to define the orthogonal decomposition for some vector $y$, where $y\in {\mathbb{R}}^n$, where $W$ is a subspace of ${\mathbb{R}}^n$, where $W^{\perp }$ is the Orthogonal Complement of $W$, where $\hat{y}$ is the orthogonal projection of $\vec{y}$ onto $W$, and $\vec{z}$ is a vector orthogonal to $\hat{y}$

$$y=(\hat{y}\in W)+(\vec{z}\in W^{\perp })$$

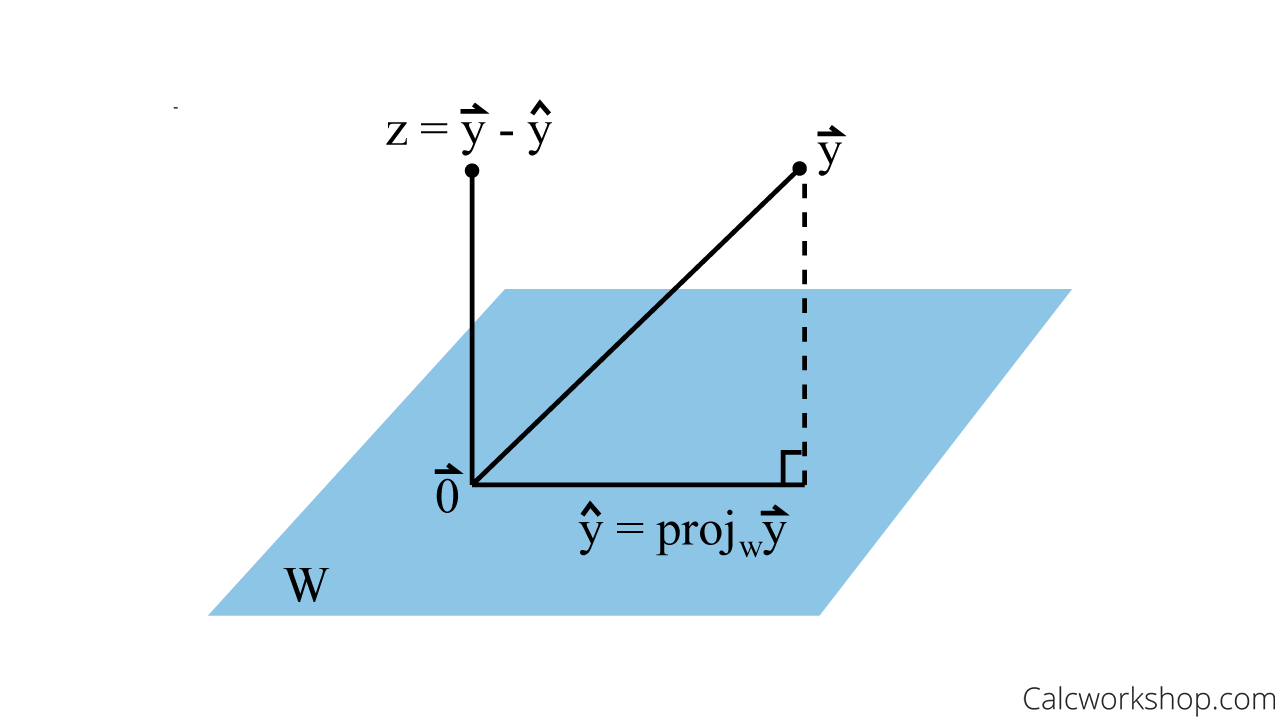
• Every $y\in {\mathbb{R}}^n$ has a unique sum in the form above, so long as $W$ is a subspace of ${\mathbb{R}}^n$
• $dim(W)+dim(W^{\perp })=n$

Concerning $\hat{y}$

If $\overrightarrow{u_1},\cdots ,\overrightarrow{u_p}$ is an Orthogonal Basis for $W$, then $\hat{y}$, the orthogonal projection of $\vec{y}$ onto $W$ is given by:

$$\begin{array}{c}\hat{y}=pro{j}_W\vec{y}=pro{j}_{\overrightarrow{u_1}}\vec{y}+\cdots +pro{j}_{\overrightarrow{u_p}}\vec{y}=pro{j}_W\vec{y}\end{array}$$

See Best Approximation, but in essence $\hat{y}$ is the closest vector in $W$ to $\vec{y}$

Examples:

HW 6.3 Q1 HW 6.3 Q5 HW 6.3 Q6