Linear Differential Equation

A Differential Equation is linear if terms appear only as

$$f(t)\cdot y^{(n)}(t)$$

Note that $y^{(n)}(t)$ is the $n^{\text{th}}$ derivative of $y(t)$ in Lagrange notation.

Linear equations can usually be solved completely and explicitly

Linear	Nonlinear
$y^{\prime }+2y=0$	$y^{\prime }+y^2=0$
$y^{\prime }+2y=t^2$	$y^{\prime }+y^2=t^2$
$y^{\prime }+t^{3}y=0$	$y^{\prime }+t{y}^3=0$
$t^2{y}^{\prime \prime \prime }-\cos (t)y^{\prime \prime }+y=0$	$y^{\prime \prime }+3y{y}^{\prime }=7\cos (t)$

First Order

A Linear Differential Equation of Order 1. We are assuming it to be a Ordinary Differential Equation.

Homogeneity

Nonhomogenous Differential Equation

$$\boxed{\frac{dy}{dt}+a(t)y=b(t)}\text{Nonhomogenous}$$

Solution Method

• Integrating Factor
• Separation of Variables General Solution

$$y(t)=C{y}_1(t)$$

where $C$ is a free parameter where $y_1(t)$ is a nonzero solution

Homogeneous Differential Equation

$$\boxed{\frac{dy}{dt}+a(t)y=0}\text{Homogenous}$$

Solution Method

• Integrating Factor General Solution

$$y(t)=y_p(t)+C{y}_1(t)$$

where $y_p(t)$ is a particular solution of the nonhomogeneous equation where $C$ is a free parameter where $y_1(t)$ is the “complementary solutions” of the corresponding homogenous equation

Integrating Factor

This method only works for First Order Linear Differential Equation, and the coefficient of the derivative must be 1. Works for both Homogeneous Differential Equation and Nonhomogenous Differential Equation. This example will use Nonhomogenous Differential Equation.

$$\begin{array}{r}\frac{dy}{dt}+a(t)y=b(t)\\ \text{Let }{A}^{\prime }(t)=a(t)\text{Let }{e}^{A(t)}y\text{ be the integrating factor}\\ e^{A(t)}y\frac{dy}{dt}+e^{A(t)}ya(t)y=e^{A(t)}yb(t)\\ \frac{d}{dt}\left(e^{A(t)}y\right)=e^{A(t)}yb(t)\\ e^{A(t)}y=\int e^{A(t)}yb(t)dt\\ y=e^{-A(t)}\int e^{A(t)}yb(t)dt+C{e}^{-A(t)}\end{array}$$

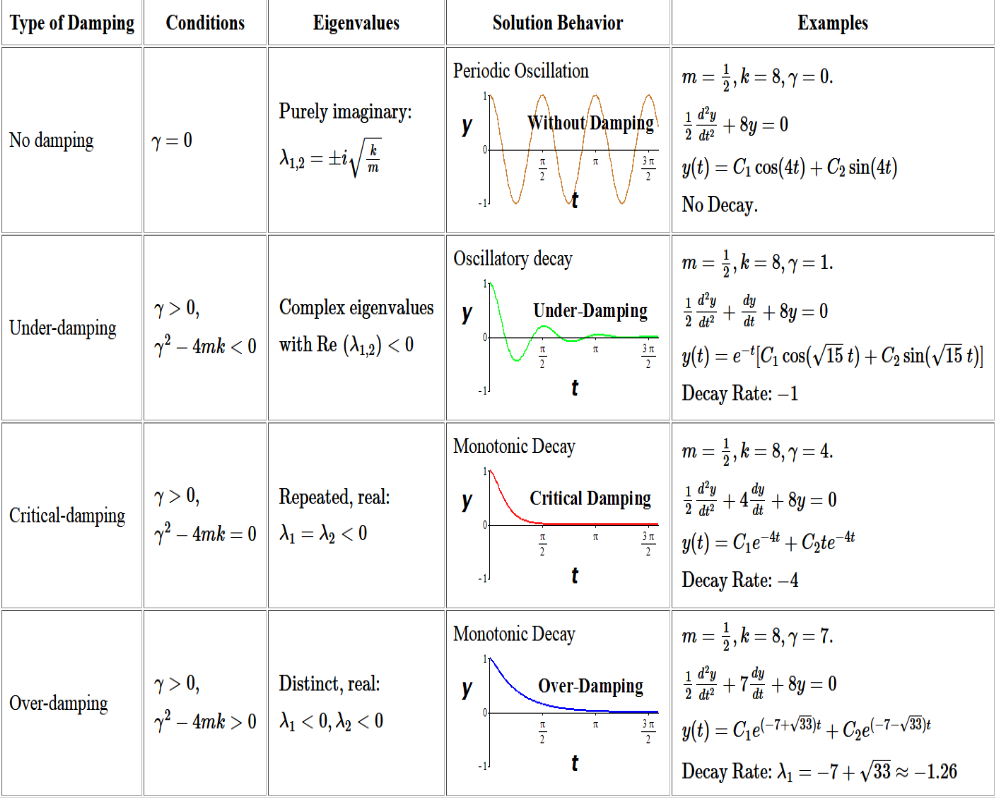
Second Order

Homogenous with Constant Coefficients

$$a{y}^{\prime \prime }+b{y}^{\prime }+cy=0$$

Specifically with this form Recall that we know how to solve 2D Homogeneous Linear Systems with Constant Coefficients

$${\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]}^{\prime }=A\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$$

Let $x_1=y,x_2=y^{\prime }$

$${\left[\begin{array}{c}y\\ y^{\prime }\end{array}\right]}^{\prime }=A\left[\begin{array}{c}y\\ y^{\prime }\end{array}\right]$$ $$\left[\begin{array}{c}{y}^{\prime }\\ y^{\prime \prime }\end{array}\right]=A\left[\begin{array}{c}y\\ y^{\prime }\end{array}\right]$$

So if we can find Linear Combination of y and y’ that yield y’ and y”, then we have transformed our 2nd order, 1 dimensional ODE into a 1st order, 2 dimensional ODE. Well we can do this. $y^{\prime }=0\cdot y+1\cdot y^{\prime }$ $y^{\prime \prime }=-\frac{c}{a}y-\frac{b}{a}{y}^{\prime }$

$$\left[\begin{array}{c}{y}^{\prime }\\ y^{\prime \prime }\end{array}\right]=\left[\begin{array}{cc}0& 1\\ -\frac{c}{a}& -\frac{b}{a}\end{array}\right]\left[\begin{array}{c}y\\ y^{\prime }\end{array}\right]$$

Great! Now we can solve this. When you’re done you can just use the first component of the vector solution and you will get $y(t)$

Also… The Characteristic Equation for this system looks very similar to the initial equation for $a=1$

$$y^{\prime \prime }+b{y}^{\prime }+cy=0⟹{\lambda }^2+b\lambda +c=0$$

But you can just do it the normal way too if you want.

Distinct Real & Nonzero Eigenvalues

$$y(t)=C_1\exp ({\lambda }_{1}t)+C_2\exp ({\lambda }_{2}t)$$

Repeated Real Eigenvalues

$$y(t)=C_1\exp (\lambda t)+C_{2}t\exp (\lambda t)$$

Complex Eigenvalues

$$y(t)=\exp (\alpha t)\left(C_1\cos (\beta t)+C_2\sin (\beta t)\right)$$

Spring Mass Problem